Viral dynamics model with CTL immune response incorporating antiretroviral therapy

Abstract

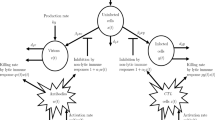
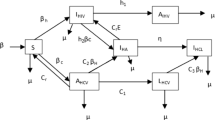
We present two HIV models that include the CTL immune response, antiretroviral therapy and a full logistic growth term for uninfected $\text{ CD4}^+$ T-cells. The difference between the two models lies in the inclusion or omission of a loss term in the free virus equation. We obtain critical conditions for the existence of one, two or three steady states, and analyze the stability of these steady states. Through numerical simulation we find substantial differences in the reproduction numbers and the behaviour at the infected steady state between the two models, for certain parameter sets. We explore the effect of varying the combination drug efficacy on model behaviour, and the possibility of reconstituting the CTL immune response through antiretroviral therapy. Furthermore, we employ Latin hypercube sampling to investigate the existence of multiple infected equilibria.

Appendices

Appendix 1

In Sect. 3, in order to obtain the number of the infected steady states, let $y:=T_{2, 1}$, then we get the following cubic equation:

$$\begin{aligned} m_1y^3+m_2y^2+m_3y+m_4=0, \end{aligned}$$

(16)

$$\begin{aligned} m_1&= \frac{rk_I}{T_{max}}>0, \\ m_2&= (d-r)k_I+\frac{rc}{T_{max}}+\frac{rk_I}{T_{max}}T^*_{2, 1} \\&= \left(\frac{\lambda }{T_0}-\frac{rT_0}{T_{max}}\right)k_I+\frac{rc}{T_{max}}+\frac{rk_I}{T_{max}}T^*_{2, 1}\\&= \frac{\lambda }{T_0}k_I+\frac{r}{T_{max}}(c-k_IT_0+k_IT^*_{2, 1}),\\ m_3&= (d-r)c+\frac{rc}{T_{max}}T^*_{2, 1}+k_I(1-\eta )N\delta T^*_{2, 1}-\lambda k_I \\&= \left(\frac{\lambda }{T_0}-\frac{rT_0}{T_{max}}\right)c+\frac{rc}{T_{max}}T^*_{2, 1}+k_I(1-\eta )N\delta T^*_{2, 1}-\lambda k_I \\&= \frac{\lambda }{T_0}(c-k_IT_0)+k_I(1-\eta )N\delta T^*_{2, 1}+\frac{cr}{T_{max}}(T_{2,1}^*-T_0), \\ m_4&= -c\lambda <0. \end{aligned}$$

Assuming $y_1, y_2$ and $y_3$ are the roots of Eq. (16), from the relationship between roots and coefficients, we know

$$\begin{aligned} y_1y_2y_3=-\frac{m_4}{m_1}>0. \end{aligned}$$

(17)

Let $f(y):=m_1y^3+m_2y^2+m_3y+m_4$, we know $f(0)=m_4<0$ and $f(+\infty )\rightarrow +\infty$. Using the intermediate value theorem, we know $f(y)=0$ has at least one positive real root. Furthermore, we can guess Eq. (16) has one positive real root or three positive real roots from (17). We know the discriminant of the cubic equation is,

$$\begin{aligned} \Delta =18m_1m_2m_3m_4-4m_2^3m_4+m_2^2m_3^2-4m_1m_3^3-27m_1^2m_4^2. \end{aligned}$$

• (a) If $\Delta =0$, then the equation has a multiple root and all its roots are real.

• (b) If $\Delta <0$, then the equation has one real root and two nonreal complex conjugate roots.

• (c) If $\Delta >0$, then the equation has three distinct real roots.

Integrating the intermediate value theorem with the discriminant, we obtain the following:

Lemma 1

• (a) If $\Delta \le 0$, then Eq. (16) has one positive real root.

• (b) If $\Delta >0$, then Eq. (16) has three distinct real roots

  • (i) if $m_2<0$ and $m_3>0$, then Eq. (16) has three distinct positive real roots;

  • (ii) if $m_2\ge 0$ or $m_3\le 0$, then Eq. (16) has one positive real root.

Proof

It is obvious to see that conclusions (a) and (ii) are satisfied. Next, we only need to prove conclusion (i).

If $\Delta >0$, assume $y_1>0, y_2$ and $y_3$ are the real roots of $f(y)=0$. To the contrary, $y_2<0$ and $y_3<0$. Then

$$\begin{aligned} f(y)&= (y-y_1)(y-y_2)(y-y_3)\\&= y^3-(y_1+y_2+y_3)y^2+(y_1y_2+y_2y_3+y_1y_3)y-y_1y_2y_3. \end{aligned}$$

Suppose that $m_2<0$, that is $y_1+y_2+y_3>0$, then $y_1>-(y_2+y_3)$. Also, suppose that $m_3>0$, that is $y_1y_2+y_2y_3+y_1y_3>0$, then $y_1(y_2+y_3)>-y_2y_3$. As $-(y_2+y_3)>0, y_1>0$, then $y_1(y_2+y_3)<-(y_2+y_3)^2$. We can get $-(y_2+y_3)^2>-y_2y_3$, that is $(y_2+\frac{1}{2}y_3)^2+\frac{3}{4}y_3^2<0$, which is a contradiction.

Appendix 2

The proof of Theorem 4.5 in Sect. 4.

Proof

The characteristic equation of system (2) at the steady state $E_{2, i}$ is

$$\begin{aligned} \xi ^4+b_{1, i}\xi ^3+b_{2, i}\xi ^2+b_{3, i}\xi +b_{4, i}=0, \end{aligned}$$

(18)

where,

$$\begin{aligned} b_{1, i}&= \alpha _{2, i}+\delta \mathcal D _{1, i}+c+ik_IT_{2, i}>0, \\ b_{2, i}&= \alpha _{2, i}(\delta \mathcal D _{1, i}+c+ik_IT_{2, i})+d_C \delta \mathcal D _{2, i} +\frac{r\delta T_{2, i}^*}{T_{max}}\mathcal D _{1, i}-ik_I\overline{k}_IV_{2, i}T_{2, i}, \\ b_{3, i}&= d_C\delta (\alpha _{2, i}+c+ik_IT_{2, i})\mathcal D _{2, i} +c\delta \mathcal D _{1, i}\left(\overline{k}_I V_{2, i} +\frac{rT_{2, i}^*}{T_{max}}\right)>0,\\ b_{4, i}&= d_C \delta \mathcal D _{2, i}[\alpha _{2, i}c+ik_IT_{2, i}(\alpha _{2, i}-\overline{k}_IV_{2, i})]. \end{aligned}$$

Using the Routh–Hurwitz criterion, we get

$$\begin{aligned} \Delta _{1, i}&= b_{1, i}>0,\\ \Delta _{2, i}&= b_{1, i}b_{2, i}-b_{3, i} \\&= \alpha _{2, i}(\alpha _{2, i}+\delta \mathcal D _{1, i}+c+ik_IT_{2, i})(\delta \mathcal D _{1, i}+c+ik_IT_{2, i}) +d_C\delta ^2 \mathcal D _{1, i}\mathcal D _{2, i}\\&+\,(\alpha _{2, i}+\delta \mathcal D _{1, i}+ik_IT_{2, i})\frac{r\delta T_{2, i}^*}{T_{max}} \mathcal D _{1, i} -c\delta \overline{k}_I \mathcal D _{1, i} V_{2, i} \\&-\,ik_I\overline{k}_IV_{2, i}T_{2, i}(\alpha _{2, i}+\delta \mathcal D _{1, i}+c+ik_IT_{2, i})\\ \!&= \! \alpha _{2, i}(c+\delta \mathcal D _{1, i})(\alpha _{2, i}+\delta \mathcal D _{1, i}\!+\!c+ik_IT_{2, i}) \!+\!(\alpha _{2, i}\!+\!\delta \mathcal D _{1, i}\!+\!ik_IT_{2, i})\dfrac{r\delta T_{2, i}^*}{T_{max}} \mathcal D _{1, i} \\&+\,ik_IT_{2, i}(\alpha _{2, i}+\delta \mathcal D _{1, i}+c+ik_IT_{2, i})(\alpha _{2, i}-\overline{k}_IV_{2, i}) +d_C\delta ^2 \mathcal D _{1, i}\mathcal D _{2, i} \\&-\,c\delta \mathcal D _{1, i}\overline{k}_IV_{2, i}\\&= \alpha _{2, i}[c^2\!+\!\delta ^2 \mathcal D _{1, i}^2\!+\!(\alpha _{2, i}\!+\!ik_IT_{2, i})(c\!+\!\delta \mathcal D _{1, i})] \!+\!d_C\delta ^2 \mathcal D _{1, i}\mathcal D _{2, i}\\&+\,(\alpha _{2, i}+\delta \mathcal D _{1, i}+ik_IT_{2, i})\dfrac{r\delta T_{2, i}^*}{T_{max}} \mathcal D _{1, i} +c\delta \mathcal D _{1, i}(2\alpha _{2, i}-\overline{k}_IV_{2, i}) \\&+\,ik_IT_{2, i}(\alpha _{2, i}+\delta \mathcal D _{1, i}+c+ik_IT_{2, i})(\alpha _{2, i}-\overline{k}_IV_{2, i}). \end{aligned}$$

In the following calculations, we will consider $i=0$ and $i=1$, respectively.

Case 1: $i=0$

$$\begin{aligned} \Delta _{3, 0}&= b_{3, 0}\Delta _{2, 0}-b_{1, 0}^2b_{4, 0}\\&= \alpha _{2, 0}d_C\delta ^2T_{crit, 0}(T_{crit, 0}-1)( \mathcal{A }+\alpha _{2, 0}\delta T_{crit, 0}) +cd_C\delta ^2T_{crit, 0}(T_{crit, 0}-1)\mathcal{A } \\&+\,cV_{2, 0}\left(\overline{k}_I\delta T_{crit, 0} \!+\!\frac{r\overline{k}_AT_{2, 0}}{T_{max}}\right) [c\alpha _{2, 0}(c\!+\!\alpha _{2, 0})\!+\!\alpha _{2, 0} \delta T_{crit, 0}(\alpha _{2, 0}\!+\!\delta T_{crit, 0})\\&+\,c\delta T_{crit, 0}(2\alpha _{2, 0}-\overline{k}_IV_{2, 0})+d_C\delta ^2T_{crit, 0}(T_{crit, 0}-1)]\\&+\,(\alpha _{2, 0}+\delta T_{crit, 0})T_{crit, 0} \frac{r\delta T_{2, 0}^*}{T_{max}}\\&\times [d_C\delta (c+\alpha _{2, 0})(T_{crit, 0}-1)+c\delta \overline{k}_IV_{2, 0}T_{crit, 0}],\\ \Delta _{4, 0}&= b_{4, 0}\Delta _{3, 0}, \end{aligned}$$

where $\mathcal A =\alpha _{2, 0}^2+d_C\delta (T_{crit, 0}-1)-c\overline{k}_IV_{2, 0}$.

We know $b_{4, 0}=\alpha _{2, 0}cd_C\delta (T_{crit, 0}-1)>0$, from the above expressions of $\Delta _{2, 0}, \Delta _{3, 0}$ and $\Delta _{4, 0}$ , we conclude that if condition (14) is satisfied, then $\Delta _{2, 0}>0, \Delta _{3, 0}>0$ and $\Delta _{4, 0}>0$. Therefore, $E_{2, 0}$ is locally asymptotically stable under condition (14).

Case 2: $i=1$. In order to simplify the following polynomial, use the factorization

$$\begin{aligned} b_{1, 1}^2&= \delta \mathcal{D }_{1, 1}(\alpha _{2, 1}+c+k_IT_{2, 1}+\delta \mathcal{D }_{1, 1})+(\alpha _{2, 1}+c+k_IT_{2, 1})(\alpha _{2, 1}+c\\&+\,k_IT_{2, 1}+\delta \mathcal{D }_{1, 1}), \end{aligned}$$

then

$$\begin{aligned} \Delta _{3, 1}&= b_{3, 1}\Delta _{2, 1}-b_{1, 1}^2b_{4, 1} \\&= \mathcal{B }_1+\mathcal{B }_2+c\delta \mathcal{D }_{1, 1}\left(\overline{k}_IV_{2, 1}+\frac{rT_{2, 1}^*}{T_{max}}\right) [\Delta _{2, 1}-d_C\delta ^2 \mathcal D _{1, 1}\mathcal{D }_{2, 1}], \end{aligned}$$

where,

$$\begin{aligned} \mathcal{B }_1&= d_C\delta \mathcal{D }_{2, 1}(\alpha _{2, 1}+c+k_IT_{2, 1})\{\Delta _{2, 1}-d_C\delta ^2\mathcal{D }_{1, 1}\mathcal{D }_{2, 1} \\&-\,(\alpha _{2, 1}+c+k_IT_{2, 1} +\delta \mathcal{D }_{1, 1})[\alpha _{2, 1}c+k_IT_{2, 1}(\alpha _{2, 1}-\overline{k}_IV_{2, 1})]\}\\&= d_C\delta ^2\mathcal{D }_{1, 1}\mathcal{D }_{2, 1}(\alpha _{2, 1}+c+k_IT_{2, 1})\left[c(\alpha _{2, 1} -\overline{k}_IV_{2, 1})\right.\\&+\left.\left(\alpha _{2, 1}+\frac{rT_{2, 1}^*}{T_{max}}\right)(\alpha _{2, 1}+k_IT_{2, 1}+\delta \mathcal{D }_{1, 1})\right],\\ \mathcal{B }_2&= d_C\delta ^2 \mathcal{D }_{1, 1}\mathcal{D }_{2, 1}\\&\{b_{3, 1}-(\alpha _{2, 1}+c+k_IT_{2, 1}+\delta \mathcal{D }_{1, 1}) [\alpha _{2, 1}c+k_IT_{2, 1}(\alpha _{2, 1}-\overline{k}_IV_{2, 1})]\},\\ \mathcal{B }_1+\mathcal{B }_2&= d_C\delta ^2\mathcal{D }_{1, 1}\mathcal{D }_{2, 1}(b_{3, 1}+\mathcal{B }_3). \end{aligned}$$

and

$$\begin{aligned} \Delta _{4, 1} = b_{4, 1}\Delta _{3, 1}. \end{aligned}$$

From the expressions of $\Delta _{2, 1}$, we know $\Delta _{2, 1}-d_C\delta ^2 \mathcal{D }_{1, 1}\mathcal{D }_{2, 1}>0$. Also, we conclude that if $\overline{k}_I V_{2, 1}<\alpha _{2, 1}$, then $b_{4, 1}>0$ and $\Delta _{2, 1}>0$. Furthermore, if $\mathcal{B }_3>0$ is satisfied, we can obtain $\Delta _{3, 1}>0$ and $\Delta _{4, 1}>0$. This completes the proof.$\square$