On Schauder estimates for a class of nonlocal fully nonlinear parabolic equations

Abstract

We obtain Schauder estimates for a class of concave fully nonlinear nonlocal parabolic equations of order $\sigma \in (0,2)$ with rough and non-symmetric kernels. We also prove that the solution to a translation invariant equation with merely bounded data is $C^\sigma$ in x variable and $\Lambda ^1$ in t variable, where $\Lambda ^1$ is the Zygmund space. From these results, we can derive the corresponding results for nonlocal elliptic equations with rough and non-symmetric kernels, which are new even in this case.

Appendix

In the “Appendix”, we first provide a sketch of the proof of Corollary 2.2.

Proof

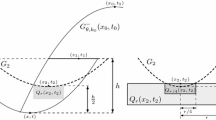
By a scaling argument, we assume that $r=1$. Let $k\ge 1$ be a constant to be determined later. Set ${\hat{\delta }}=\delta /k$. Let $(t_0,x_0)\in \overline{Q_{\delta /2}}$ be such that $u(t_0,x_0)=\inf _{Q_{\delta /2}}u$. Since $\sigma \in (1,2)$, we have $2^{-\sigma }\le 1-4^{-\sigma }$. By a scaling and translation of the coordinates, we apply Proposition 2.1 to u in $Q_{{\hat{\delta }}}(t_0,x_0)$ and obtain

$$\begin{aligned} {{\hat{\delta }}}^{-(\sigma +d)/\varepsilon }\Vert u\Vert _{L_\varepsilon ({\hat{Q}}_1)} \le C_1\Big (\inf _{Q_{{\hat{\delta }}}(t_0,x_0)}u+C{\hat{\delta }}^\sigma \Big ), \end{aligned}$$

where ${\hat{Q}}_1=Q_{{\hat{\delta }}}(t_1,x_0)$ and $t_1=t_0-(4^\sigma -1){{\hat{\delta }}}^\sigma$. For any $x_1\in B_{{\hat{\delta }}/2}(x_0)$,

$$\begin{aligned}&\Vert u\Vert _{L_\varepsilon ({\hat{Q}}_1)}\ge \Vert u\Vert _{L_\varepsilon ((t_1-\delta ^\sigma ,t_1 )\times B_{{\hat{\delta }}/2}(x_1))}\\&\quad \ge C_2{\hat{\delta }}^{(\sigma +d)/\varepsilon }\inf _{(t_1-\delta ^\sigma ,t_1 )\times B_{{\hat{\delta }}/2}(x_1)}u\ge C_2{\hat{\delta }}^{(\sigma +d)/\varepsilon }\inf _{Q_{{{\hat{\delta }}}}(t_1,x_1)}u, \end{aligned}$$

where $C_2>0$ depending only on d. Therefore,

$$\begin{aligned} \inf _{Q_{{{\hat{\delta }}}}(t_1,x_1)}u\le C_1/C_2\Big (\inf _{Q_{{\hat{\delta }}}(t_0,x_0)}u+C{\hat{\delta }}^\sigma \Big ) . \end{aligned}$$

Applying Proposition 2.1 again, we have

$$\begin{aligned} {{\hat{\delta }}}^{-(\sigma +d)/\varepsilon }\Vert u\Vert _{L_\varepsilon ({\hat{Q}}_2)} \le C_1\Big (\inf _{Q_{{\hat{\delta }}}(t_1,x_1)}u+C{\hat{\delta }}^\sigma \Big ), \end{aligned}$$

where ${\hat{Q}}_2=Q_{{\hat{\delta }}}(t_2,x_1)$ and $t_2=t_0-2(4^\sigma -1){{\hat{\delta }}}^\sigma$, and for any $x_2\in B_{{{\hat{\delta }}}/2}(x_1)$,

$$\begin{aligned} \inf _{Q_{{{\hat{\delta }}}}(t_2,x_2)}u\le C_1/C_2 \Big (\inf _{Q_{{\hat{\delta }}}(t_1,x_1)}u+C{\hat{\delta }}^\sigma \Big ). \end{aligned}$$

By induction, or any $x_{n-1}\in B_{(n-1){{\hat{\delta }}}/2}(x_0)\cap B_1$,

$$\begin{aligned}&{{\hat{\delta }}}^{-(\sigma +d)/\varepsilon }\Vert u\Vert _{L_\varepsilon ({\hat{Q}}_n)} \le C_3 \Big (\inf _{Q_{{\hat{\delta }}}(t_0,x_0)}u+C{\hat{\delta }}^\sigma \Big )\\&\quad \le C_3 \big (u(t_0,x_0)+C{\hat{\delta }}^\sigma \big ) =C_3 \Big (\inf _{Q_{\delta /2}}u+C{\hat{\delta }}^\sigma \Big ), \end{aligned}$$

where ${\hat{Q}}_n=Q_{{\hat{\delta }}}(t_{n},x_{n-1})$, $t_{n}=t_0-n(4^\sigma -1){\hat{\delta }}^\sigma$, and $C_3$ is a constant depending only on $\lambda$, $\Lambda$, d, and n. Notice that $|x_0|\le \delta /2$, $t_0\in [-(\delta /2)^\sigma ,0]$, and $\sigma >1$. We can choose $k\ge 1$ in a suitable range depending only on $\sigma _2$ and $\delta$, and then $n\le [2k/\delta ]+1$, such that ${{\hat{Q}}}_n$ runs through $(-\delta ^\sigma ,-\delta ^\sigma +(4^\sigma -1){\hat{\delta }}^\sigma )\times B_1$. Finally, by applying Proposition 2.1 again and using a simple covering argument, we prove the corollary. $\square$

Finally, we give the proofs of Lemmas 5.1, 5.2, and 5.3.

Proof of Lemma 5.1

By mollification, it suffices to prove (5.2) assuming that $f\in C^\alpha ((-1,0))$. Let $x,y\in (-1,0)$, $y<x$, and $h:=x-y$. When $h\ge 1/3$,

$$\begin{aligned} \frac{|f(x)-f(y)|}{h^\alpha }\le 2\cdot 3^\alpha \Vert f\Vert _{L_\infty ((-1,0))}. \end{aligned}$$

When $h<1/3$, either $x<-1/3$ or $y>-2/3$. If $x<-1/3$, then $2x-y\in (x,0)$ and

$$\begin{aligned} \frac{|f(x)-f(y)|}{h^\alpha }&\le \frac{1}{2}\frac{|f(2x-y)+f(y)-2f(x)|}{h^\alpha } +\frac{1}{2}\frac{|f(2x-y)-f(y)|}{h^\alpha }\\&\le \frac{3^{\alpha -1}}{2}[f]_{\Lambda ^1((-1,0))} +\frac{1}{2^{1-\alpha }}[f]_{\alpha ;(-1,0)}. \end{aligned}$$

The case when $y>-2/3$ is similar. Therefore,

$$\begin{aligned}{}[f]_{\alpha ;(-1,0)}\le 2\cdot 3^\alpha \Vert f\Vert _{L_\infty ((-1,0))}+\frac{1}{2^{1-\alpha }}[f]_{\alpha ;(-1,0)} +\frac{3^{\alpha -1}}{2} [f]_{\Lambda ^1((-1,0))}, \end{aligned}$$

which yields (5.2). $\square$

Proof of Lemma 5.2

First we consider the case when $\beta =1$. Integrating by part and noting that $\eta ''$ is an even function and $\int \eta ''=0$, we obtain

$$\begin{aligned}&\big |\partial _t^2u^{(R)}\big | =\Big |\int _{{\mathbb {R}}}\big (2\partial _t^2 u(t-R^\sigma s,x) -\partial _t^2 u(t-2R^\sigma s,x)\big )\eta (s-1)\,ds\Big |\\&\quad =\Big |\int _{{\mathbb {R}}}R^{-2\sigma } \Big (2u(t-R^\sigma s,x)-\frac{1}{4} u(t-2R^\sigma s,x)\Big ) \eta ''(s-1)\,ds\Big |\\&\quad =\Big |\int _{{\mathbb {R}}}R^{-2\sigma } \Big (u(t-R^\sigma s,x)+u(t-R^\sigma (2-s),x)-2u(t-R^\sigma ,x)\\&\qquad -\frac{1}{8} \big (u(t-2R^\sigma s,x)+u(t-2R^\sigma (2-s),x)-2u(t-2R^\sigma ,x)\big )\Big ) \eta ''(s-1)\,ds\Big |\\&\quad \le CR^{-\sigma }[u]^t_{\Lambda ^1}. \end{aligned}$$

For $\beta \in (0,1)$, when $r\ge R^\sigma$,

$$\begin{aligned} r^{-1-\beta }|u^{(R)}(t,x)+u^{(R)}(t-2r,x)-2u^{(R)}(t-r,x)| \le r^{-\beta }[u]^t_{\Lambda ^1}\le R^{-\beta \sigma }[u]^t_{\Lambda ^1}. \end{aligned}$$

When $r\in (0,R^\sigma )$, by (5.3) with $\beta =1$,

$$\begin{aligned}&r^{-1-\beta }|u^{(R)}(t,x)+u^{(R)}(t-2r,x)-2u^{(R)}(t-r,x)| \le r^{1-\beta }[\partial _t u^{(R)}]^t_{1;{\mathbb {R}}^{d+1}_0}\\&\quad \le Cr^{1-\beta }R^{-\sigma }[u]^t_{\Lambda ^1}\le CR^{-\beta \sigma }[u]^t_{\Lambda ^1}. \end{aligned}$$

From the above two inequalities, we immediately get (5.3). $\square$

Proof of Lemma 5.3

We first estimate the Hölder semi-norm in x. By the interpolation inequality,

$$\begin{aligned}&[u-p]_{\alpha ;(-R^\sigma ,0)\times B_{2^jR}}^*\nonumber \\&\quad \le (2^jR)^{-\alpha }\Vert u-p\Vert _{L_\infty ((-R^\sigma ,0)\times B_{2^jR})}+(2^jR)^{\sigma -\alpha }[u-p]^*_{\sigma ;(-R^\sigma ,0)\times B_{2^jR}}. \end{aligned}$$

(5.17)

Because p is linear,

$$\begin{aligned}{}[u-p]^*_{\sigma ;(-R^\sigma ,0)\times B_{2^jR}}=[u]^*_{\sigma ;(-R^\sigma ,0)\times B_{2^jR}}. \end{aligned}$$

(5.18)

Since $\eta$ has unit integral, we have

$$\begin{aligned}&\big |u^{(R)}(t,x)-u(t,x)\big |\nonumber \\&\quad =\Big |\int _{{\mathbb {R}}}\big (2u(t-R^\sigma s,x)-u(t-2R^\sigma s,x) -u(t,x)\big )\eta (s-1)\,ds\Big |\le CR^\sigma [u]^t_{\Lambda ^1}. \end{aligned}$$

(5.19)

Furthermore, for any $(t,x)\in (-R^\sigma ,0)\times B_{2^jR}$,

$$\begin{aligned}&\big |u^{(R)}(t,x)-p(t,x)\big | =\big |u^{(R)}(t,x)-u^{(R)}(0,0)-\partial _tu^{(R)}(0,0)t -x^TDu^{(R)}(0,0)\big |\\&\quad \le \big |u^{(R)}(t,x)-u^{(R)}(t,0)-x^TDu^{(R)}(t,0)\big |\\&\quad +\big |u^{(R)}(t,0)-u^{(R)}(0,0)-\partial _tu^{(R)}(0,0)t\big | +\big |x^TDu^{(R)}(0,0)-x^TDu^{(R)}(t,0)\big |\\&\quad \le (2^jR)^\sigma [u]^*_{\sigma }+R^{2\sigma } \big \Vert \partial ^2_tu^{(R)}\big \Vert _{L_\infty (-R^\sigma ,0)\times B_{2^jR}}+C2^jR^{\sigma }\big [Du^{(R)}\big ]^t_{\frac{\sigma -1}{\sigma }}. \end{aligned}$$

Using Lemma 5.2, we have

$$\begin{aligned} \big \Vert u^{(R)}-p\big \Vert _{L_\infty ((-R^\sigma ,0)\times B_{2^jR})}\le C(2^jR)^\sigma [u]^*_{\sigma }+C2^jR^{\sigma }[Du]^t_{\frac{\sigma -1}{\sigma }} +CR^\sigma [u]_{\Lambda ^1}^t, \end{aligned}$$

which together with (5.19) implies that

$$\begin{aligned} \Vert u-p\Vert _{L_\infty ((-R^\sigma ,0)\times B_{2^jR})} \le C(2^jR)^\sigma [u]^*_{\sigma }+C2^jR^{\sigma }[Du]^t_{\frac{\sigma -1}{\sigma }} +CR^\sigma [u]_{\Lambda ^1}^t. \end{aligned}$$

(5.20)

We plug (5.18) and (5.20) in (5.17) and get (5.4).

Next we estimate the Hölder semi-norm in t. Obviously,

$$\begin{aligned}{}[u-p]^t_{\alpha /\sigma ;(-R^\sigma ,0)\times B_{2^jR}}\le [u-p]^t_{\alpha /\sigma ;(-2^{j\sigma /2}R^\sigma ,0)\times B_{2^jR}}. \end{aligned}$$

From Lemma 5.1 and scaling, we have

$$\begin{aligned}&[u-p]^t_{\alpha /\sigma ;(-2^{j\sigma /2}R^\sigma ,0)\times B_{2^jR}}\\&\quad \le C(2^{j/2}R)^{-\alpha }\Vert u-p\Vert _{L_\infty ((-2^{j\sigma /2}R^\sigma ,0)\times B_{2^jR})}+C(2^{j/2}R)^{\sigma -\alpha }[u-p]^t_{\Lambda ^1} \\&\quad \le C(2^{j/2}R)^{-\alpha }\Vert u-p\Vert _{L_\infty ((-2^{j\sigma /2}R^\sigma ,0)\times B_{2^jR})}+C(2^{j/2}R)^{\sigma -\alpha }[u]^t_{\Lambda ^1}. \end{aligned}$$

We follow the proof of (5.20) to estimate

$$\begin{aligned}&\Vert u-p\Vert _{L_\infty ((-2^{j\sigma /2}R^\sigma ,0)\times B_{2^jR})}\\&\quad \le \Vert u-u^{(R)}\Vert _{L_\infty ((-2^{j\sigma /2}R^\sigma ,0)\times B_{2^jR})}+\Vert u^{(R)}-p\Vert _{L_\infty ((-2^{j\sigma /2}R^\sigma ,0)\times B_{2^jR})}\\&\quad \le CR^\sigma [u]^t_{\Lambda ^1}+C(2^jR)^\sigma [u]^*_\sigma +C2^{j\sigma }R^\sigma [u]^t_{\Lambda ^1}+C2^{j(\sigma +1)/2}R^\sigma [D {u}]^t_{\frac{\sigma -1}{\sigma }}. \end{aligned}$$

Therefore, we reach (5.5). The lemma is proved. $\square$

Proof of Lemma 5.4

We modify the proof of Lemma 5.3. Similar to Lemma 5.1, we have

$$\begin{aligned}&[u-p]_{\alpha ,\alpha ;(-R,0)\times B_{2^jR}} \le [u-p]_{\alpha ,\alpha ;Q_{2^jR}}\nonumber \\&\quad \le (2^jR)^{-\alpha }\Vert u-p\Vert _{L_\infty (Q_{2^jR})} +(2^jR)^{1-\alpha }[u-p]_{\Lambda _1;Q_{2^jR}}\nonumber \\&\quad \le (2^jR)^{-\alpha }\Vert u-p\Vert _{L_\infty (Q_{2^jR})} +(2^jR)^{1-\alpha }[u]_{\Lambda _1}. \end{aligned}$$

(5.21)

Since $\eta$ and $\zeta$ have unit integral and $\zeta$ is radial, we have

$$\begin{aligned}&\big |u^{(R)}(t,x)-u(t,x)\big |\nonumber \\&\quad =\Big |\int _{{\mathbb {R}}^{d+1}}\big (2u(t-R s,x-Ry)-u(t-2R s,x-Ry) -u(t,x)\big )\eta (s-1)\zeta (y)\,dy\,ds\Big |\nonumber \\&\quad =\Big |\int _{{\mathbb {R}}^{d+1}}\big (2u(t-R s,x-Ry)-u(t-2R s,x-Ry) -u(t,x-Ry)\big )\nonumber \\&\qquad +\frac{1}{2} \big (u(t,x+Ry)+u(t,x-Ry) -2u(t,x)\big )\eta (s-1)\zeta (y)\,dy\,ds\Big |\nonumber \\&\quad \le CR[u]_{\Lambda ^1}. \end{aligned}$$

(5.22)

For any $(t,x)\in Q_{2^jR}$, similar to Lemma 5.2 with $\beta =\alpha /2$,

$$\begin{aligned} \big |u^{(R)}(t,x)-p(t,x)\big | \le (2^jR)^{1+\alpha /2}[u^{(R)}]_{1+\alpha /2,1+\alpha /2;Q_{2^jR}} \le 2^{j(1+\alpha /2)}R[u]_{\Lambda ^1}, \end{aligned}$$

which together with (5.22) implies that

$$\begin{aligned} \Vert u-p\Vert _{L_\infty ((-2^jR,0)\times B_{2^jR})} \le 2^{j(1+\alpha /2)}R[u]_{\Lambda ^1}. \end{aligned}$$

(5.23)

We plug (5.23) in (5.21) and get (5.6). The lemma is proved. $\square$